Estimating Parallel Resistor Circuits

without a Calculator, and still have less than 5% error!

(no Slide-Rules, Log-Tables, or Calculators needed!)

03/11/2007

Forward:

Here is an example of a procedure that may seem at first a little bit awkward or confusing, and initially learning to use that process may take just a little bit of practice. Even though this process is for only 2 resistors at a time, any experience at all will allow you to pair up 2 and then pair up the result with another resistor ... and so on.

Bear in mind that it is the using of a particular technique or that makes it worthwhile to learn. You will find that all the "old-timers" in this business, because of their long term experience, instinctively use some of these methods without necessarily thinking about the process they are using at the time. If you should ask them how they do it, they may very well say "lots of experience", rather than trying to explain exactly how.

Well, here's how you can learn in a short while, what it took them otherwise years to accomplish. You will be amazed with what just a little bit of practice with these examples will allow you to do.

Method #1

I call this one the "Upper-Limit" vs "Lower-Limit" method. [ For 2 resistors of values that are less than a 2:1 ratio to each other ]

Method #2

I call this one the "Ratio-Plus-1" method. [ For 2 resistors of values that are less than a 10:1 ratio to each other ]

Method #3

I call this one the "Sliver" (or very small slice) method. [ For 2 resistors of values that are more than a 10:1 ratio to each other ]

A special note:

These 3 methods may seem at first to be somewhat awkward, but they are actually very effective. It is only because of the necessary wording and lengthy explanations that are necessary here, that may make them appear awkward. They do take just a little bit of getting used to, but just a little bit of practice will allow you to quickly and easily approximate resultant values that are surprisingly close to what they should be.

1. "Upper-Limit" vs "Lower-Limit" method:
[ For 2 resistors of values that are less than a 2:1 ratio to each other ]

{To practice this exercise, you need to draw a sketch of 2 resistors in parallel}

• Everyone learns early that 2 parallel resistors of the same value will simply result in a value of 1/2 of either.

     PDF File

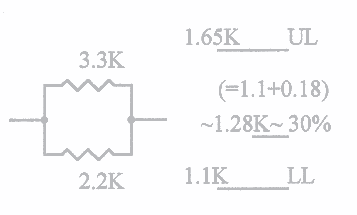
• To illustrate the simplicity of our method, consider that if we had 2 parallel 2.2K resistors, the resultant value of these would simply be 1.1K, and if we had 2 parallel 3.3K resistors, the resultant value would be a little over 1.65K. (remember, we are only interested in approximations, so don't get too picky!).
• The first interesting thing is that we consider that if we had a 2.2K in parallel with a 3.3K, we know that the lowest resultant value would be as if there were 2 of the 2.2K's....and the highest resultant value would be as if there were 2 of the 3.3K's.
• The 1.1K represents what we can call our "Lower-Limit", and the 1.65K is what we would call our "Upper-Limit"
• This simply means that our resultant parallel value will lie somewhere between the 1.1K and the 1.65K !!
• The next interesting observation, is that the actual value for this 2 resistor combination will be close to 1/3 of the difference, and above the 1.1K "Lower-Limit".
• I.e. The difference between 1.65K and 1.1K is 0.55K, and 1/3rd of this difference is about 0.18K, so if we simply add this 0.18K to the "Lower-Limit" of 1.1K, we would get close to 1.28K as our approximate result. (Actually, I kinda fudged here a little, in that I know that 1/3 of 0.60K would be 0.20K, so I fudged it down some from the 0.20K, and guessed at about 0.18K)
• Now if you use the conventional formula to compute the actual correct answer, you will get 1.32K, which means that we were 97% correct, or if you wish, only an error of 3% !! Remember also, that the resistors you buy are usually only accurate to 5%.
• You will find that the results of this method of approximation will work for any 2 parallel resistors, providing that they are within a 2:1 ratio of each other.
• For 2 parallel resistors that are greater than a 2:1 ratio, this method does not work well, but there are others that do.

2. "Ratio + 1" method:
[ For 2 resistors of values that are greater than a 2:1 ratio, but less than a 10:1 ratio to each other ]

{To practice this exercise, you need to draw a sketch of 2 resistors in parallel}

• This method is quite straight forward, in that you approximate the ratio of the 2 resistors that are in parallel with each other, and add 1 to that ratio.

     PDF File

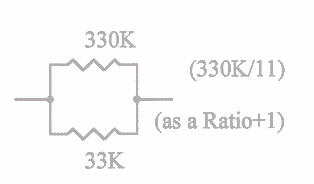
• Example: Take a 33K resistor and a 330K resistor, place them in parallel with each other. It should be obvious that the ratio between those 2 resistors is 10:1.
• Now take that 10:1 ratio, add 1 to make it 11:1.
• Divide the larger of the 2 resistor values (which is the 330K) by the 11 of the new ratio, and the result will be 30K !!
• Of course, with approximating the ratio of real resistor values can be apparently a little sloppy, but you will be amazed just how close you can be. Remember, we are only approximating these results, but practice really helps.
• Another example: Take a 3.9K and a 6.8K and place them in parallel with each other. Since I personally don't like to even try to figure really odd values, I simply consider the 3.9K as almost 4K and the 6.8K as almost 7K. Now, that ratio might be just a little less than a simple 2:1 ratio, so I'll call my "Ratio + 1" a little less than a 3:1.
• Now, simply divide the larger of those 2 parallel resistors (the 6.8K) by my <3, and approximate the result as approximately 2.4K.
• Remember that when you divide a number by something "less than", your result will be "more than", which is why when we might have taken the 6.8K (think of the 6.8K as 6.9K for easy division) and divided it by less than the 3:1 ratio, we will get a number that is more than the expected 2.3K. We can call it approximately 2.4K.
• Now, if you calculate the actual result by conventional means, the result will be found to be about 2.479K.
• This means that we estimated an answer that turned out to be 96.8% correct, and therefore only an error of 3.2% !!

This method does take a little more practice than the "Lower-Limit" vs "Upper-Limit" method, to get a good handle on it, but with practice..........

A special note: This method, done with a calculator, is a 3rd method not commonly given in the text books, but is accurate.

3. "Sliver" method:
[ For 2 resistors of values where one is greater than a 10:1 ratio to the other ]

{To practice this exercise, you need to draw a sketch of 2 resistors in parallel}

In presenting this method, I like to illustrate what I call the difference between "Fudge-Factor" and "Finagle's-Constant", where the "Fudge-Factor" is when you discover an error in your calculations that can be brought into line by "Fudging" your answer by just the right amount... Now, suppose that you somehow knew ahead of time that your resultant answer was going to be slightly wrong (and about how much), and you determined that if you could "Finagle" the parameters ahead of time, and then you wouldn't have to "Fudge" later. Hmmm....

First, we need to explain our "Finagle-Parameters":

• It can be considered that an error caused by disregarding a parallel resistor which has a value of 10 times more than the first resistor (i.e. a 10:1 ratio) will cause a 10% error.
• It can also be considered that by disregarding parallel resistors of a 100:1 ratio will cause only a 1% error.
• Finally, it can be considered that disregarding parallel resistors of a 1000:1 will cause only a 0.1% error.

Here we can see that if we can estimate the amount of possible error ahead of time, we can simply remove a "Sliver" off of the lowest value, with the size of the "Sliver" depending on the amount of expected error.

      PDF File

• Example #1: Place a 27K in parallel with a 270K resistor. Now if we disregarded the 270K resistor and called the result 27K, we would be in error because the result is always "less than the least". But, if we knew that ahead of time, we could simply take about a 10% slice ("Sliver") off of the 27K (which is 2.7K), and we wind up with an approximate value of 24.3K as a result. [24.54K actual, for 99% accuracy ]
• Example #2: Place a 4.7K in parallel with a 680K resistor. Don't worry about the actual ratio. Just consider it at about 100:1. Again, if we disregarded the 680K effect, we would be in error (but not very much). Now, take a 1% slice ("Sliver") off of the 4.7K (which is 0.047K), and we wind up with an approximate value of 4.65K as a result. [4.67K actual, for 99.6% accuracy]
• Example #3: Place a 3.9K in parallel with a 2.7Meg. Now, we know that the 2.7Meg is not going to affect the actual value by very much. In fact, it will only drop the 3.9K by about 0.1%, which is only a drop of about 3.9ohms from the 3.9K. We would do this by taking off a slice of that 0.1% (3.9ohms) from the 3.9K, to give us an approximate value of 3.89K. [3.89K actual, for 100% accuracy]

You may have noticed some variations in what I described, vs what was shown in the schematics, as well as the fact that if you carried out the calculations with a calculator, you would find some apparent discrepancies. But remember that these are "approximations", and some allowable slop (if you want to call it that ) is not a problem!
PDF File of all 3 Examples (20Kb)