Thevenin's and Norton's Equivalent Circuits

07/14/2001

Introduction

We often make a bad assumption that the voltage source we are using will give us a reliable and consistent voltage to our respective loads and their variances. To avoid this error, we need to understand what is going on in our sources. These might include everything from batteries for various vehicles, lawnmowers, electronics equipment, and even toys. There is a special source where we charge certain types of batteries, where we want to control the amount of current instead of controlling the voltage.

In evaluating the performance of voltage sources we will discover that the Thevenin's Analysis is the most useful, and where we are trying to evaluate the performance of current control we will discover that the Norton's Analysis is the most useful.

We need to be aware that "current control" should not be confused with "supplying various amounts of current depending on the load". This special situation is based on the concept that the current delivered to the load will remain constant, regardless of what voltage is required. A more thorough explanation will be found in the Norton's Equivalent section.

Thevenin's Equivalent Circuit:

Commonly used for evaluating voltage variations, under various loads and the current variations drawn by the load.

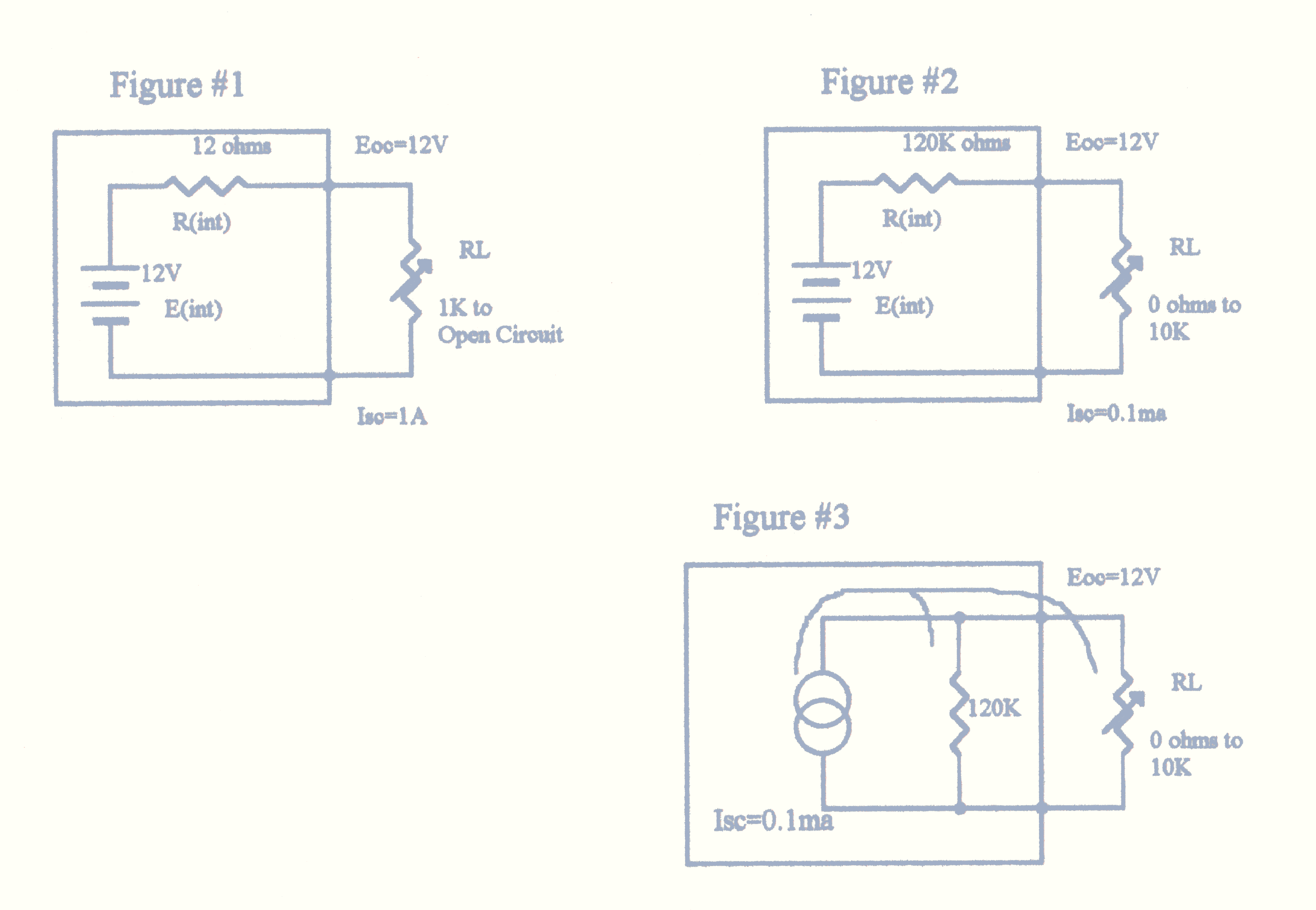
In Figure #1, the internal resistance R(int) of the source is much lower than the resistance of the load RL, therefore the majority of the source voltage E(int) will be available to the load. This situation (where there is a high resistance ratio) allows the source to be considered as a "Constant Voltage Source". Just how good though is another matter. We need to remember that in Figure #1 that the voltage across the load will be nearly 12V, but that some of the source voltage will be dropped across the internal resistance. We should also recognize that the lower the internal resistance is, compared to the load resistance, the less voltage loss we will experience internally, and therefore the better will be our "Constant Voltage Source".

There is a practical "rule-of-thumb" that we can refer to, that refers to the actual resistance ratio, that you won't normally find in the textbooks. Consider that there are 3 principle comparisons, where a ratio of 10:1 is only "Fair", a ratio of 100:1 is "Good", and a ratio of 1,000:1 could be considered as "Excellent".

In simple terms, this means that with the values given in Figure #1, we would assign our "Constant Voltage Source" as a "Good Constant Voltage Source". If the internal resistance was even lower (say about 1.2 ohms), we would see a resistance ratio of close to 1,000:1, and that would give us an even better "Constant Voltage Source", i.e. an "Excellent Constant Voltage Source".

In summary, there are no "perfect" Constant-Voltage-Sources, but we can determine or predict the expected outcome of this circuit, if we understand the true relationships.

One last consideration for the moment... It should be obvious that if our load resistance was the same as our internal resistance, we would find that the voltage divides evenly between them, causing 6V across each, and also that the resulting current flow through the load would be 1/2 of the maximum (Isc).

Norton's Equivalent Circuit

Commonly used for evaluating current variations, under various loads and the variations in the voltages required.

In Figure #2, the internal resistance R(int) of the source is much higher than the resistance of the load RL, therefore determines the amount of current that will be available through the load. It is not a question of delivering lots of current, but rather keeping the current flow relatively constant, even with changes in the load. This situation (where there is a high resistance ratio) allows the source to be considered as a "Constant Current Source". Just how good though is another matter. We need to remember that in Figure #2 that the current through the load will actually be determined by the 12V source and the internal resistance of 120K, and that the load resistance plays only a very little part. We should also recognize that the higher the internal resistance is, compared to the load resistance, the less the change of the load will affect the actual amount of current flow, and therefore the better will be our "Constant Current Source".

Here again there is the practical "rule-of-thumb" that we can refer to, which refers to the actual resistance ratio, that you won't normally find in the textbooks. Consider those same 3 principle comparisons, where a ratio of 10:1 is only "Fair", a ratio of 100:1 is "Good", and a ratio of 1,000:1 could be considered as "Excellent".

In simple terms, this means that with the values given in Figure #2, we would assign our "Constant Current Source" as a "Good Constant Current Source". If the internal resistance was even higher (say about 1.2 Megohms), we would see a resistance ratio of close to 1,000:1, and that would give us an even better "Constant Current Source", i.e. an "Excellent Constant Current Source".

In summary, there are no "perfect" Constant Current Sources, but we can determine or predict the expected outcome of this circuit, if we understand the true relationships.

There is another method of looking at the Constant Current Source that is quite valuable, and unfortunately this is the one that often confuses folks (Figure #3). If approached correctly though, it's not confusing at all, and once understood it turns out to be a very valuable method indeed. Not only that, but we'll show you that when we approach it correctly, we find that we can easily convert easily and directly from one to the other. The circuit just looks a little strange, but remember that this is a "equivalent circuit" that represents the actual or physical circuit.

Consider that we can have a source where instead of a voltage source, we have a current source that always delivers the same amount of current. If the load were a short circuit, then all of the current would be delivered to the load, with none going through the 120K shown. On the other hand, if the load were removed, providing an open circuit, all of the source current would go through the 120K and develop the same Eoc as in Figure #2!

Again, one last consideration for the moment... It should be obvious that if our load resistance was the same as our internal resistance, we would find that the current divides evenly between them with the resulting current flow through the load being 1/2 of the maximum (Isc). Note that this gives exactly the same type of results as the Thevenin's Equivalent Circuit.

Converting from Thevenin's directly to Norton's, and vice-versa

Even though the Thevenin's Equivalent Circuit Analysis is the most practical method for evaluating Constant Voltage Sources, it can also be used for accurately analyzing Constant Current Sources.

In like manner, the Norton's Equivalent Circuit Analysis is the most practical method for evaluating Constant Current Sources, it can can be also used for accurately analyzing Constant Voltage Sources.

A special note here is that the internal resistance R(int) for the Thevenin's is exactly the same for the Norton's.

To determine the Norton's Equivalent Circuit from a Thevenin's Equivalent Circuit, simply determine the amount of current that would flow through a short circuit placed as the load. Where an open load (i.e. no current flow) would give what is called the "Eoc" across the supply terminals, a short circuit load would cause the maximum current flow through the load (i.e. and no voltage) called the "Isc". This "Isc" is the Constant Current described as the Norton's Source.

To determine the Thevenin's Equivalent Circuit from a Norton's Equivalent Circuit, simply determine the amount of voltage that would occur across the supply terminals of the current source with the load removed.

In summary, the "Eoc" for both representations would be the same, and the "Isc" for both representations would be the same.